拓扑排序简介

发表于

简介

拓扑排序是一种针对有序无环图的排序方法，其会将一个有序无环图转化为一条链，且对于有序无环图中的每一条边u -> v，都保证节点u在节点v之前出现，即在将原图转化为一条链的过程中不破坏节点的先后顺序。

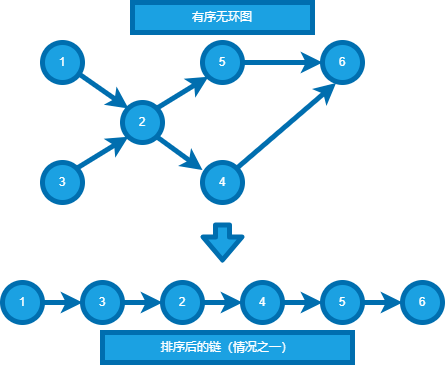
拓扑排序示例

可以看到，上图中的链中节点的先后顺序仍然保持原样。

需要注意的是：一个有环的图是没法进行拓扑排序的，这很好理解，因为u -> v和v -> u的路径同时出现的话，u和v在链内就没有任何一种合法的排序方法，自然也无法排序。

前置知识：度

顶点的度是指某个顶点连出的边数。特别地，在有向图中，入度是指以该顶点为终点的有向边数量；顶点的出度是指以顶点为起点的有向边数量。
度

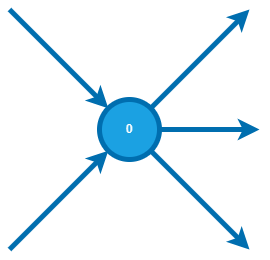
上图展示了一个入度为2，出度为3的点

同时，很容易知道，在一个有向图中所有节点的入度之和和出度之和相等。

算法实现（C++）

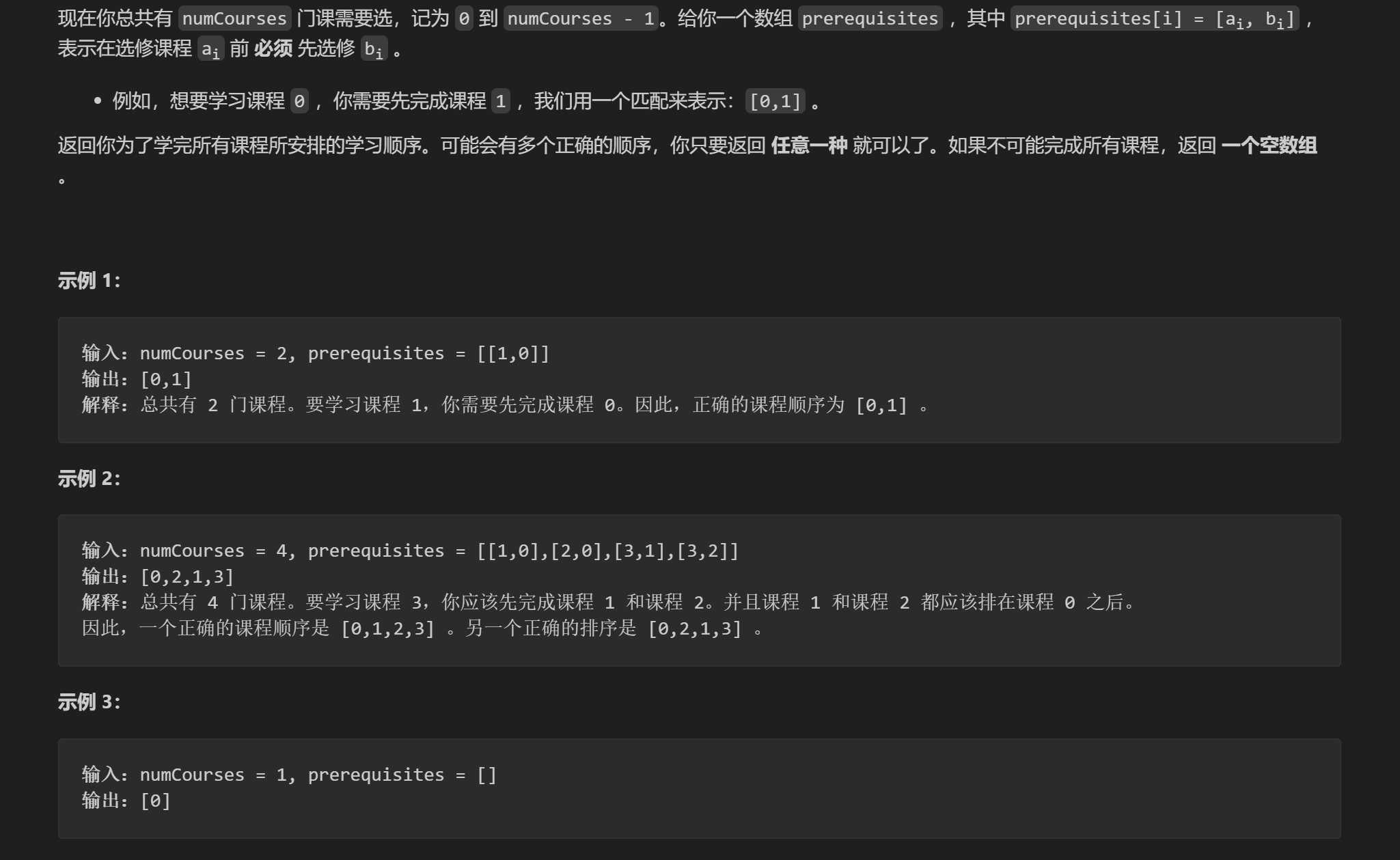
以LeetCode上第210题【课程表II】为例，根据题面信息，我们可以知道这是一道实现拓扑排序的题目。

题面信息

实现拓扑排序的一个基本思路是使用广度优先搜索，其基本流程和思路如下：

  1. 求解每个顶点的入度并储存
  2. 开始循环，首先将当前状态下所有入度为0的点加入链中
    由于这样的点没有任何指向于它的边存在，故将其加入链必然不与节点之间的先后顺序矛盾。
  3. 将刚才加入了链的点在图中删除，减少与其有关联的点的入度
    因为这个点已经加入了链，故在它之后加入的点相对于它而言就一定是合法的，故在图中取消这个点对接下来其它节点的限制。
  4. 回到循环，检查在刚才的操作中入度变为0的节点，再执行相同的操作
  5. 直到发现所有节点都被添加入链或剩下的节点没有一个入度为0（图带环），结束循环，返回结果

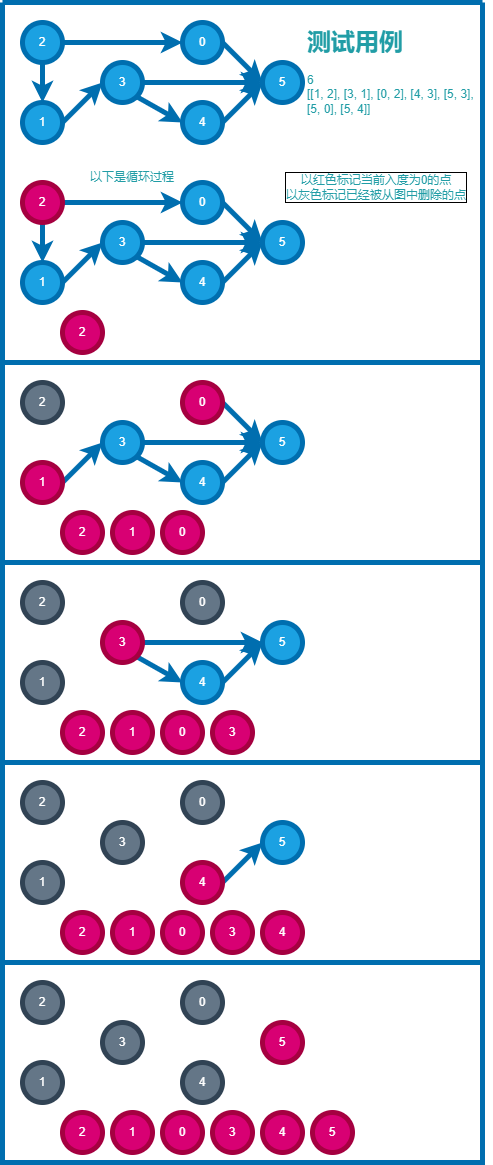
以下是一张示例图，展示了用BFS实现拓扑排序的一个进行过程。

广度优先搜索实现拓扑排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/*
 * @lc app=leetcode.cn id=210 lang=cpp
 *
 * [210] 课程表 II
 */
#include <vector>
#include <queue>
#include <unordered_map>
using namespace std;
// @lc code=start
class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<int> indegrees; indegrees.resize(numCourses, 0);
        unordered_map<int, vector<int>> links;
        for (int i = 0; i < prerequisites.size(); i++) {
            indegrees[prerequisites[i][0]]++; // 统计所有节点的入数
            if (links.find(prerequisites[i][1]) == links.end()) {
                links.insert(pair<int, vector<int>>(prerequisites[i][1], vector<int>()));
            }
            links[prerequisites[i][1]].push_back(prerequisites[i][0]); // 使用哈希表记录节点连接关系
        }
        // 开始广度搜索，每个回合把入度为0的节点加入链中
        vector<int> result;
        queue<int> openNodes;
        while (true) {
            for (int i = 0; i < indegrees.size(); i++) {
                if (!indegrees[i]) {
                    result.push_back(i);
                    openNodes.push(i);
                    indegrees[i] = -1; // 这个点已经进链，将其入度设置为-1，不检查之
                }
            }
            if (openNodes.empty()) {
                if (result.size() == numCourses) { return result; }
                else { return vector<int>(); } // 返回结果
            }
            while (!openNodes.empty()) {
                vector<int> connected = links[openNodes.front()];
                for (int node : connected) { indegrees[node]--; }
                openNodes.pop(); // 将入度为0的点从图中删除
            }
        }
    }
};

后记

以上就是拓扑排序的大致介绍，在实际情况中，它常用来解决关键路径问题（AOE网络），在此不作详细展开。

总之感谢您的阅读！