游戏碰撞检测算法：SAT（分离轴定理）的C#实现

发表于 2024-03-07 更新于 2024-03-25

介绍：SAT为何物

简介

在游戏开发的过程中，我们往往会进行碰撞检测。 SAT（Separating Axis Theorem，分离轴定理）是一种常用的碰撞检测算法。运用它，我们可以对任意凸多边形、圆之间进行碰撞检测。

原理

介绍其原理前，我们先来看在数学上的凸集分离定理，它是SAT算法的基础。

凸集
凸集是对于集合内的每一对点，连接该对点的直线段上的每个点也在该集合内。
超平面
超平面是指n维线性空间中维度为n-1的子空间。它可以把线性空间分割成不相交的两部分。
对于三维空间来说，超平面就是一个二维平面，对于二维平面，超平面就是一条直线。
凸集分离定理
两个不相交的凸集总可用超平面分离。

注：上述定理的证明我也不会，这需要用到大学的数学知识，然而我连大专学历都没有（

引申

根据上述原理，我们可以得到在二维平面上的分离轴定理

对于两个凸多边形，若存在一条直线将两者分开，则这两个多边形不相交。

接下来，我们将会用程序去寻找这条直线，找到了，两个多边形就会分离，反之为碰撞。

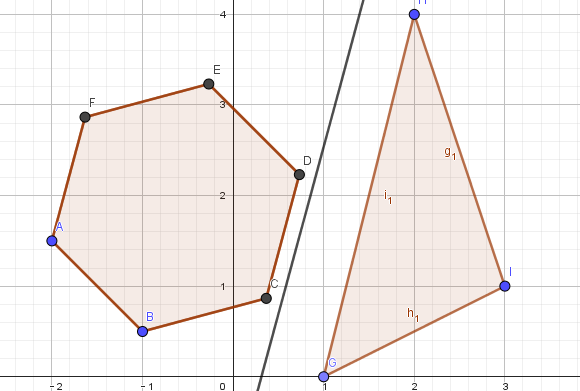
图中给出了一个实例，两个分开的凸多边形被一条直线分开

讨论：SAT算法的实现逻辑

我们的检验方法可以概括为：

对于两个凸多边形，检测是否存在一条这样的直线t：

作垂直于t的直线l，将两个多边形的所有顶点分别投影到l上；
分别做出两个多边形的最远的两个投影点的连接线；
如果两条连接线不存在相交部分，则此时两个多边形在直线t的方向上存在一条直线分割两个多边形

只要有一条这种直线t，那么两个凸多边形就算是分离了。

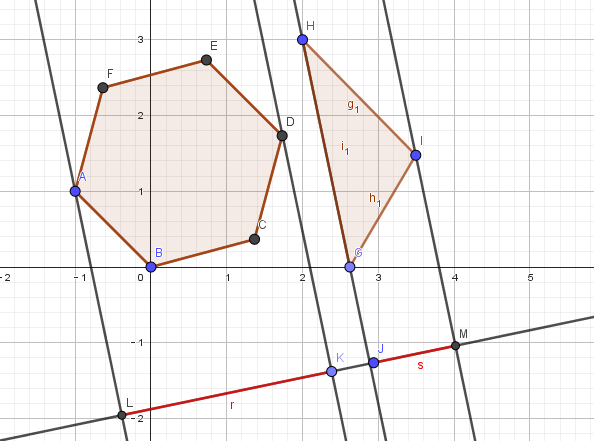
这是投影的示意图，可以看到，两个多边形分离。

不过，程序的算力不允许我们遍历所有方向，那么在这里，我们将该方法做一种简化，我们只需要将所有的多边形的边的方向作为直线t的方向，其垂线作为投影轴（直线l）即可。

将两个多边形所有的边所在的直线作为直线t进行依次测试，
如果都不行，则再不存在其它的直线满足条件。
其实就是，只需要依次在每条边的垂直线做投影即可。

此外，圆和多边形之间的碰撞检测大体相同，只不过我们还需要加一条投影轴（直线l），是圆心到多边形上距离圆心最近一点的连线。

注：我们的数学直觉告诉我们确实是这样的，但是要证明这样做可行，还是比较困难的。（就是我不会的意思。）

于是，检测碰撞的过程就是：

依次确定多边形的各个投影轴；
将多边形投射到某条投影轴上；
检测两段投影是否发生重叠。

实现：SAT算法的C#代码

定义

首先，我们需要定义几个类来帮助我们表示多边形、圆。

using System;
using Microsoft.Xna.Framework;

/// <summary>
/// 多边形
/// </summary>
public class Polygon {

    private Vector2[] points;
    /// <summary>
    /// 投影轴列表
    /// </summary>
    private Line[] verticleLines;
    public Vector2[] Points { get => points; }
    public Line[] VerticleLines { get => verticleLines; }

    /// <summary>
    /// 创建多边形
    /// </summary>
    /// <param name="points">顶点</param>
    public Polygon(Vector2[] points) {
        if (points.Length <= 1) { throw new Exception("多边形的顶点数应当大于1"); }
        this.points = new Vector2[points.Length];
        for (int i = 0; i < points.Length; i++) {
            this.points[i] = new Vector2(points[i].X, points[i].Y);
        }
        FillVerticleLines();
    }

    /// <summary>
    /// 创建多边形的所有投影轴
    /// </summary>
    private void FillVerticleLines() {
        verticleLines = new Line[Points.Length];
        for (int i = 0; i < Points.Length - 1; i++) {
            var edge = new Line(Points[i], Points[i + 1]);
            verticleLines[i] = ShapeManager.ReturnVerticleLine(edge, Vector2.Zero);
            // 这里的ReturnVerticleLine方法过会会给出
        }
        verticleLines[Points.Length - 1] = ShapeManager.ReturnVerticleLine
        (new Line(Points[Points.Length - 1], Points[0]), Vector2.Zero);
        // 所有的投影轴都过原点，且与某一条边垂直
    }

    /// <summary>
    /// 获取多边形的所有边
    /// </summary>
    /// <returns></returns>
    public Line[] GetAllEdges() {
        Line[] edges = new Line[Points.Length];
        for (int i = 0; i < Points.Length - 1; i++) {
            var edge = new Line(Points[i], Points[i + 1]);
            edges[i] = edge;
        }
        edges[Points.Length - 1] = new Line(Points[Points.Length - 1], Points[0]);
        return edges;
    }
}

/// <summary>
/// 圆形
/// </summary>
public class Circle {

    /// <summary>
    /// 圆心
    /// </summary>
    public Vector2 center;
    /// <summary>
    /// 半径
    /// </summary>
    public float radius;

    /// <summary>
    /// 创建一个圆形
    /// </summary>
    /// <param name="point">圆心</param>
    /// <param name="radius">半径</param>
    public Circle(Vector2 point, float radius) {
        center = point;
        this.radius = radius;
    }
}

/// <summary>
/// 线段
/// </summary>
public class Line {

    /// <summary>
    /// 端点1
    /// </summary>
    public Vector2 point1;
    /// <summary>
    /// 端点2
    /// </summary>
    public Vector2 point2;

    /// <summary>
    /// 创建一条线段
    /// </summary>
    /// <param name="point_1">起点</param>
    /// <param name="point_2">终点</param>
    public Line(Vector2 point_1, Vector2 point_2) {
        point1 = point_1;
        point2 = point_2;
    }

}

如上方所示，我们用Polygon和Circle两个类表示多边形和圆，还添加了Line表示线段。

Polygon储存多边形的顶点points，并且在创建之初就提供了所有边相应的投影轴verticleLines，这是由FillVerticleLines()方法给出的，多边形还有GetAllEdges方法获取所有的边；
Circle储存一个圆的对象，具有center圆心坐标，radius半径数据；
Line储存一条线段的两个顶点point1``point2的位置；
Vector2表示一个向量，具有X Y表示其水平、竖直分量，它来自MonoGame Framework。（我平常游戏开发所使用的就是这个框架。）

判断

我们定义一个ShapeManager类来对它们做判断，接下来我将展示其中的一些方法。

/// <summary>
/// 获取线段的垂线
/// </summary>
/// <param name="target">目标线段</param>
/// <param name="point">垂线过的点</param>
internal static Line ReturnVerticleLine(Line target, Vector2 point) {
    if (!target.IsZeroVector()) {
        Vector2 swiftPos = target.point2 - target.point1;
        Vector2 normalVector = new Vector2(-swiftPos.Y, swiftPos.X);
        normalVector.Normalize();
        // 获取线段的法向量
        return new Line(point, point + normalVector);
    }
    return new Line(new Vector2(point.X, point.Y), new Vector2(target.point1.X, target.point1.Y));
}

前文提到了ReturnVerticleLine()方法，现在在此给出，它返回一条过顶点的垂线，用于确定投影轴。
这里涉及到了Normalize()方法，这会将normalVector转化为单位向量（模长为1）。

/// <summary>
/// 判断两个多边形是否发生碰撞
/// </summary>
public static bool IsCollision(Polygon polygon1, Polygon polygon2) {
    var allVerticles = new Line[polygon1.VerticleLines.Length + polygon2.VerticleLines.Length];
    Array.Copy(polygon1.VerticleLines, 0, allVerticles, 0, polygon1.VerticleLines.Length);
    Array.Copy(polygon2.VerticleLines, 0, allVerticles, polygon1.VerticleLines.Length, polygon2.VerticleLines.Length);
    // 合并两个投影轴数组
    foreach (Line verticle in allVerticles) {
        float[] cast1 = GetProjectLengthRange(polygon1, verticle);
        float[] cast2 = GetProjectLengthRange(polygon2, verticle);
        if (!IsTwoProjectionIntersect(cast1, cast2)) {
            return false;
        }
    }
    return true;
}

这是IsCollision()方法，它用于判定两个多边形是否相交。

首先，获得所有可能的投影轴，将它们储存在allVerticles内；
接着，用GetProjectLengthRange()，将它们依次投影到轴上，每条轴都来一遍；
用IsTwoProjectionIntersect()判断，如果有一条轴出现分离，认为两个多边形分离。

接下来，我们来具体看一下后两个方法的实现。

关键方法

/// <summary>
/// 获取圆关于指定投影轴的投影长度取值范围
/// </summary>
/// <param name="circle">被投影圆</param>
/// <param name="castOn">投影轴</param>
private static float[] GetProjectLengthRange(Circle circle, Line castOn) {
    float projectValue = circle.center.X * (castOn.point1.X - castOn.point2.X) +
    circle.center.Y * (castOn.point1.Y - castOn.point2.Y);
    float[] result = new float[2] { projectValue - circle.radius, projectValue + circle.radius };
    return result;
}

在这个方法中，我们对起始位置为原点，末位置为多边形顶点的向量和投影轴向量进行了相乘，获得了它们的数量积。由于ReturnVerticleLine()获取的投影轴方向向量是单位向量，结合高中知识，这个数量积表示投影点到投影轴向量起始点（在这里是原点）的距离，那么所有投影点其距离的最大、最小值就可以表示线段的位置。

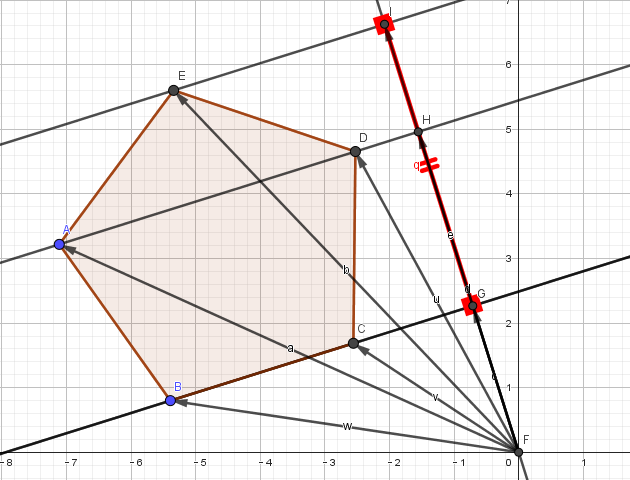
就是这样，我们获取了线段端点到原点的位置，进而确定线段。

/// <summary>
/// 检测两个投影线段是否相交
/// </summary>
private static bool IsTwoProjectionIntersect(float[] cast1, float[] cast2) {
    float minAll = MathF.Min(cast1[0], cast2[0]);
    float maxAll = MathF.Max(cast1[1], cast2[1]);
    return cast1[1] - cast1[0] + (cast2[1] - cast2[0]) >= maxAll - minAll;
    // 如果两条线段中间有空隙，总线段长度大于二线段之和，否则，二线段有相交部分
}

接下来根据线段的位置判断，就没有问题了。

圆的特殊投影轴

当然，根据前文所说，我们在判断圆和多边形相交时，要新加入一条投影轴，那么根据其性质，代码如下。

/// <summary>
/// 判断圆与多边形之间是否发生碰撞
/// </summary>
public static bool IsCollision(Polygon polygon, Circle circle) {
    var allVerticles = new Line[polygon.VerticleLines.Length + 1];
    Array.Copy(polygon.VerticleLines, 0, allVerticles, 0, polygon.VerticleLines.Length);
    allVerticles[allVerticles.Length - 1] = GetNearestAxisFromPolygon(circle.center, polygon);
    foreach (Line verticle in allVerticles) {
        float[] cast1 = GetProjectLengthRange(polygon, verticle);
        float[] cast2 = GetProjectLengthRange(circle, verticle);
        if (!IsTwoProjectionIntersect(cast1, cast2)) {
            return false;
        }
    }
    return true;
}

/// <summary>
/// 获取点到多边形最近点的投影轴
/// </summary>
private static Line GetNearestAxisFromPolygon(Vector2 point, Polygon polygon) {
    float nowDistance = float.MaxValue;
    Line axis = new Line(Vector2.Zero, Vector2.Zero);
    // 对每一条边做判断
    Line[] edges = polygon.GetAllEdges();
    foreach (Line edge in edges) {
        float distance = GetDistanceFromPointToLine(point, edge);
        if (distance < nowDistance) {
            nowDistance = distance;
            axis = ReturnVerticleLine(edge, Vector2.Zero);
            // 发现距离边最近，投影轴为边的法向量
        }
    }
    // 对每一个点做判断
    foreach (Vector2 polygonPoint in polygon.Points) {
        float distance = Vector2.Distance(polygonPoint, point);
        if (distance < nowDistance) {
            nowDistance = distance;
            var pointer = point - polygonPoint;
            pointer.Normalize();
            axis = new Line(Vector2.Zero, pointer);
            // 发现距离点最近，那么点之间的向量为投影轴
        }
    }
    return axis;
}

/// <summary>
/// 获取点到直线距离
/// </summary>
private static float GetDistanceFromPointToLine(Vector2 point, Line line) {
    // 获取三角形面积
    Polygon triangle = new Polygon(new Vector2[3] {point, line.point1, line.point2});
    float area = triangle.GetTriangleArea();
    // 获取底面长度
    float edgeLength = Vector2.Distance(line.point1, line.point2);
    return 2 * area / edgeLength;
}

/*
在Polygon中存在GetTriangleArea()方法
/// <summary>
/// 返回三角形面积
/// </summary>
private float GetTriangleArea(Polygon triangle) {
    Vector2[] trianglePoints = triangle.Points;
    if (trianglePoints.Length != 3) {
        throw new Exception("三角形必须只具有三个顶点：" + trianglePoints);
    }
    // 海伦公式
    float p = (trianglePoints[0].Length() +
    trianglePoints[1].Length() + trianglePoints[2].Length()) / 2;
    return MathF.Sqrt(p * (p - trianglePoints[0].Length()) *
    (p - trianglePoints[1].Length()) * (p - trianglePoints[2].Length()));
}
*/

如上，我们就找到了圆心到多边形上最近一点的连线的方向向量，因而确定了那条特殊的投影轴。

完整代码查看

欢迎访问我的个人项目FullLeafFramework，一个以MonoGame为基础的游戏框架扩展，在dev分支上，你可以下载到拥有以上逻辑判断的完整代码，这里只是截取关键部分帮助理解。

总结

SAT是一种非常有效的凸多边形、圆的碰撞检测算法，可以做到对凸多边形、圆是否相交的精密检测，其复杂度为O((m+n)^2)，在多边形边数不多时效率不错，但一旦边数过大便效率有限，且它对于凹多边形不适用，使用时需注意。